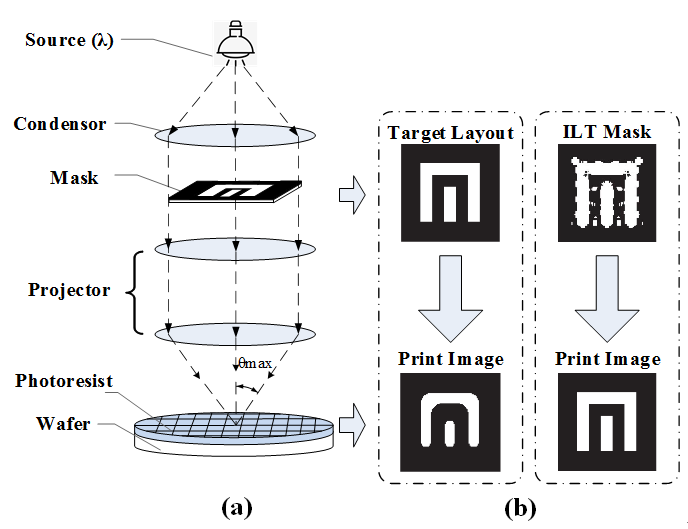
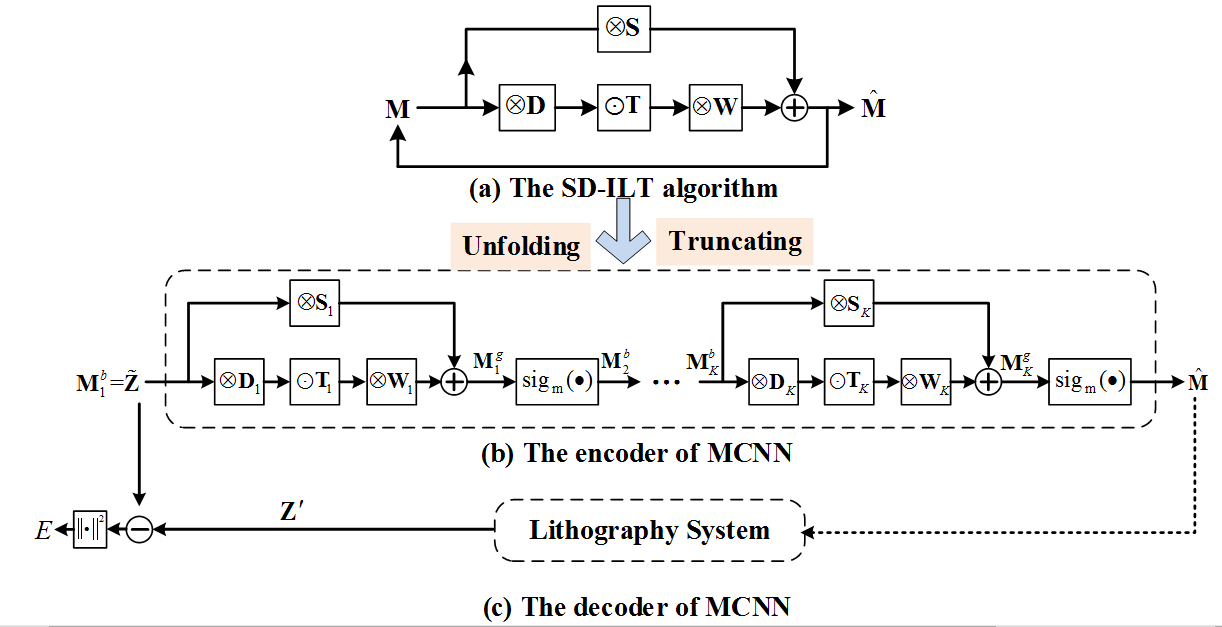
Optical lithography is a crucial technology to manufacture the integrated circuits (IC) in semiconductor industry. Figure 1(a) shows the schematic diagram of a typical deep-ultraviolet (DUV) optical lithography system, which is used to transfer the IC layouts from photomask onto wafer
[1, 2]. The illumination of DUV lithography system emits the light rays with 193nm wavelength, which pass through the optical lens and uniformly illuminate the photomask. The transmitted light rays from mask are collected by the projection optics, and then form the aerial image on the wafer. On the top surface of wafer there is a thin layer of photo-sensitive material, namely photoresist that is exposed and developed. Finally, the IC layout pattern is replicated on the wafer after etch process.
As the critical dimensions (CD) continuously shrink, computational lithography has been widely used to improve the resolution of wafer image and extend the life of Moore’s Law
[3]. Computational lithography refers to a set of technologies that design and optimize lithography systems and processes through mathematical and algorithmic approaches. Inverse lithography technology (ILT) is a representative computational lithography approach that compensates image distortion by pre-warping the photomask patterns. ILT regards the mask pattern as a binary pixelated image, where the zero-valued and one-valued pixels represent opaque and transparent regions, respectively. Figure 1(b) presents an illustration of ILT method
[4]. Pixel-based ILT greatly improves the degrees of freedom in mask optimization, so it can effectively improve the imaging performance of lithography systems.
Figure 1.
(a) The sketch of deep ultraviolet optical lithography system, and (b) the illustration of ILT method (revised from Fig. 1 in Ref. [5]). In the past, researchers have proposed a number of gradient-based algorithms to solve the ILT problems
[6, 7]. For instance, Liu et al. compensated the image distortion for both binary mask and phase-shifting mask using the branch and bound algorithm, as well as the simulated annealing algorithm
[8]. Sherif et al. proposed a binary mask optimization method for incoherent diffraction-limited imaging system, where the problem was formulated as a mixed linear integer program (MLIP), and then the branch and bound method was used to solve the problem
[9]. Granik et al. formulated ILT as nonlinear, constrained minimization problems over a domain of mask pixels, and then applied local variation and gradient descent methods to quickly solve ILT problems
[4]. Poonawala et al. proposed a set of gradient-based algorithms and regularization methods to solve the ILT problem in coherent lithography imaging system
[7]. However, traditional gradient-based ILTs have to face with the great challenges of large amount of computation and low efficiency
[10].
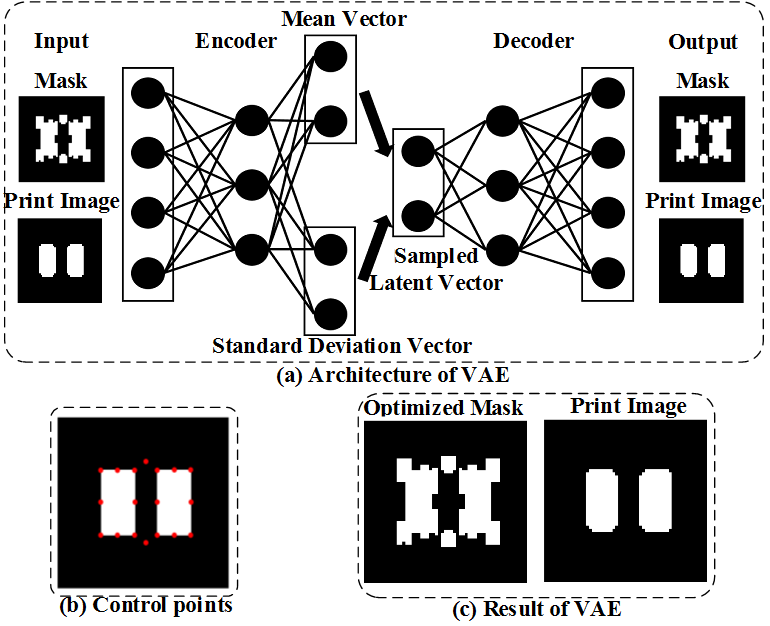
In order to overcome the computational complexity, many machine learning techniques have been applied to accelerate the ILT algorithms
[11]. Wang et al. used machine learning to efficiently generate sub-resolution assist features (SRAF) on full-chip layout at 20nm technology node, and achieved a high imaging accuracy
[12]. Guajardo et al. used machine learning methods to jointly optimize the main features (MF) and SRAFs
[13]. Ma et al. proposed fast mask optimization algorithms based on non-parametric kernel regression, which can effectively improve the computational efficiency and mask manufacturability
[14]. Xu et al. proposed a fast SRAF generation method that involved support vector machines (SVM) and logistic regression models in the complete mask optimization process
[15]. K. Luo et al. and R. Luo et al. respectively proposed fast mask optimization methods based on SVMs
[16] and multilayer perceptual neural networks
[17].
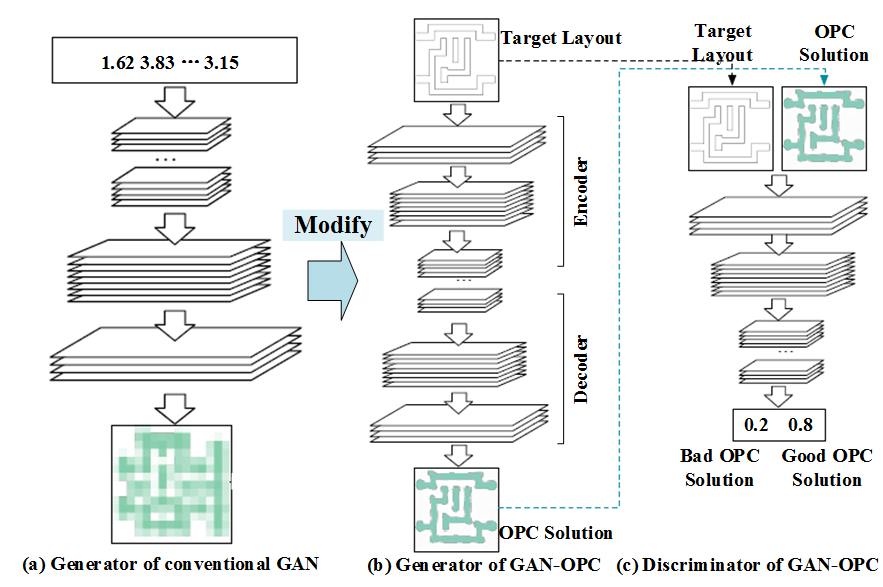
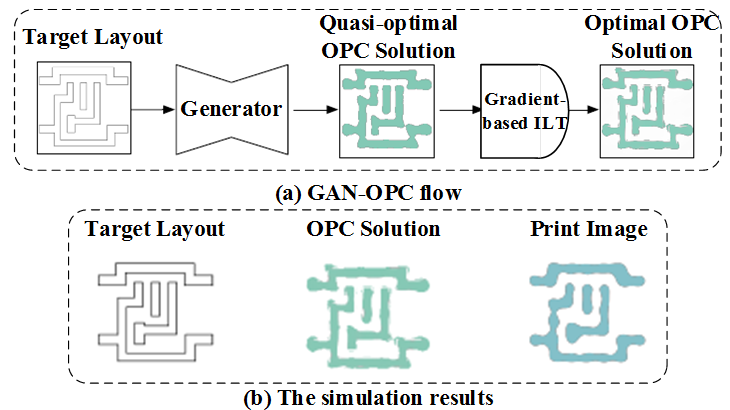
Due to the high nonlinearity of ILT problem, traditional machine learning methods have their inherent limitations. For instance, traditional machine learning methods often require a large number of training samples to accurately construct the nonlinear mapping between the IC layout and the corresponding ILT solution
[10]. In the latest decade, deep learning has become the forefront of fast ILT approaches, since it can properly fit any complex nonlinear function
[18]. This paper will describe and discuss in detail several ILT methods based on deep learning.
The rest of this paper is organized as follows. Section 2 summarizes the ILT methods based on standard deep learning approaches, and Section 3 describes and discusses several ILT methods based on a radically new learning method, namely model-driven convolution neural network (MCNN). The paper will be concluded in Section 4.