To evaluate the time scale of intermixing and its dependence on the initial state of the structure and process conditions, a kinetic model of the system must be developed. For this endeavor, one might be tempted to employ the same MD approach used to calculate the energy of the system as described above. However, directly integrating equations of motion for all atoms in the solid results in issue with the time scales involved. To resolve thermal vibrations of atoms, i.e. phonons, one needs to limit the time step at least by the inverse of the typical phonon frequency, which in practical simulations of solids appears to be ~10
-2 ps. However, diffusion of atoms in solids is inherently a slow process; observable concentration changes occurs at a time scale closer to ~10
-3 sec
[33]. The result is that the MD approach becomes computationally prohibitive for modeling solid state diffusion. Another significant caveat is that the FF used in MD simulation would need to be specially fit to reproduce states with atoms far from their equilibrium positions in the crystal lattice, to capture hopping between sites, and not just for the equilibrium properties discussed in Section 3.1. To overcome these issues, the kinetic Monte Carlo (KMC) method
[34] can be applied. In this method, a restricted set of physical events is selected and the appropriate rates are calculated for each of event. A Monte Carlo method is then used to sample events and advance the state of the system. In the simplest version of this method, lattice KMC (KLMC), atoms can take only fixed positions in the ideal crystal lattice. An open source implementation of the KLMC is available called SPPARKS
[35]. To simulate interdiffusion, we use a customized version implemented with a model known as the binary alloy with vacancies (ABV)
[36] model. In this model, a lattice site can be occupied by either atom of type A or B or remain vacant. A simple Hamiltonian, limited to only nearest neighbor interactions, is expressed as a sum of bond energies and depends on six parameters whose values can be fitted to pure metal formation energies, the energy of insertion a foreign atom or the mixing enthalpy, and the energy of vacancy formation. While rather simple, the model allows important observations about the behavior of the system. First, the possibility of mixing is directly related to the sign of AB bond energy; positive values prevent mixing. For interdiffusion to proceed, a sufficient concentration of vacancies must be assigned to the initial state, but not so that high that vacancies can coalesce and form voids. Fortunately, the final configuration is insensitive to the initial distribution of vacancies due to their high mobility. Typically the average time step is ~10
-12-10
-13 sec unless the Metropolis MC algorithm
[37] is selected, which effectively minimizes the system energy to reach the final configuration. These simulations don’t require significant computational resources, e.g. a system of ~10
5 atoms simulating with SPPARKS using 4-8 parallel processes takes <20 min to reach the final state after ~10
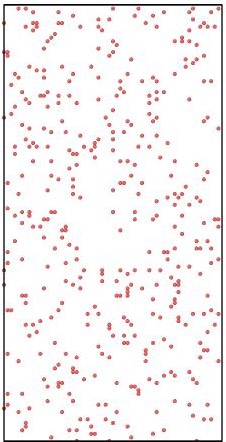
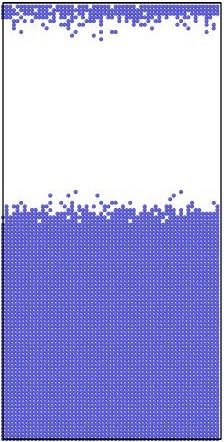
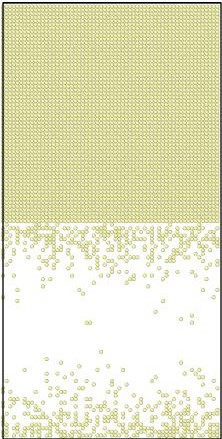
8 diffusion events. Some examples of simulation results are shown in Figure 2 for the case of good mixing of Al and Cu. The pictures have been created using OVITO
[38] which is a very useful tool for visualizing atomistic simulation results.
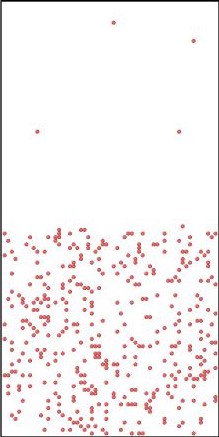
Figure 2.
Initial (top 3 panels) and final (bottom 3 panels) states for Al (blue), Cu (yellow), and vacancies (red) shown left to right respectively. The final states after using KLMC to simulate 108 diffusion events in ~10μs . Periodic boundary conditions are set in all directions to avoid a free surface. An Cu-Al alloy forms along the interface separating initially pure metals while vacancies, which are distributed uniformly at the beginning of simulation, move into the Al region. The KLMC method offers some insights into the kinetics of the intermixing although the experimental data
[24] suggest that it’s a much more complex process. Specifically, the main assumption in the KLMC model that atoms hop between sites in a rigid lattice is questionable. During processing, the lattice distorts and many intermediate phases of alloy are formed along the interface. Also, for technology applications, it’s sometimes of interest to evaluate metals with different lattice types and imperfect crystal barrier layers, i.e. those with a grain structure. To address these problems, the off-lattice KMC model
[39] has gained attention. KMC differs from KLMC in that it tracks the evolution of the system energy landscape, allowing atoms to occupy any local energy and hop through saddle-points between them. The locations of the minima and corresponding transition barriers are calculated on-the-fly using a suitable FF after every diffusion event, which makes the method extremely numerically expensive; identical systems take ~10
3 times longer to simulate with KMC versus KLMC, limiting its use
[40]. The art of creating a practical KMC code is all about handling fast diffusion events
[41], making full use of parallel computing
[42], and avoiding barriers recalculation wherever possible
[43]. As we have found at Intel, the pay-off of KMC is the quantitative agreement with experiment for interdiffusion coefficients and activation energies and the qualitative impact of lattice type, orientation, and grain boundaries. An example of its application is illustrated in Figure 3, which shows a FCC Cu - FCC Al bilayer separated with 25A of BCC Ta following 5 μs anneal at 700K. A bridge of Cu and Al atoms formed along the grain boundary through the barrier layer can be clearly seen after 4 days of modeling using 16 parallel processes. It’s also evident that the perfect crystalline Ta is all but immiscible with both Cu and Al.
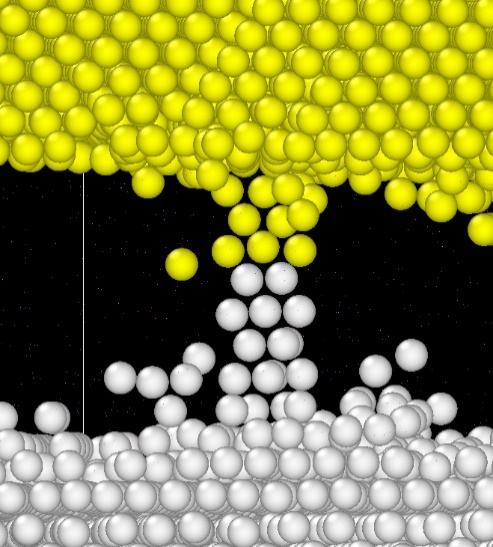
Figure 3.
The bridge of Al (white) and Cu (yellow) atoms growing through Ta (hidden) separation layer along the grain boundary. It should be noted that the MD method, despite its limitations, is being used for these type of simulations
[25,26]. While certain assumptions help make these simulations more applicable, a pure metal EAM FF is not sufficient for interdiffusion simulations. The FF must include cross-type interactions of metal atoms
[44] or hybridization as available in MD codes such as LAMMPS
[12].
4. Metal Deposition for Electronic Property Calculations
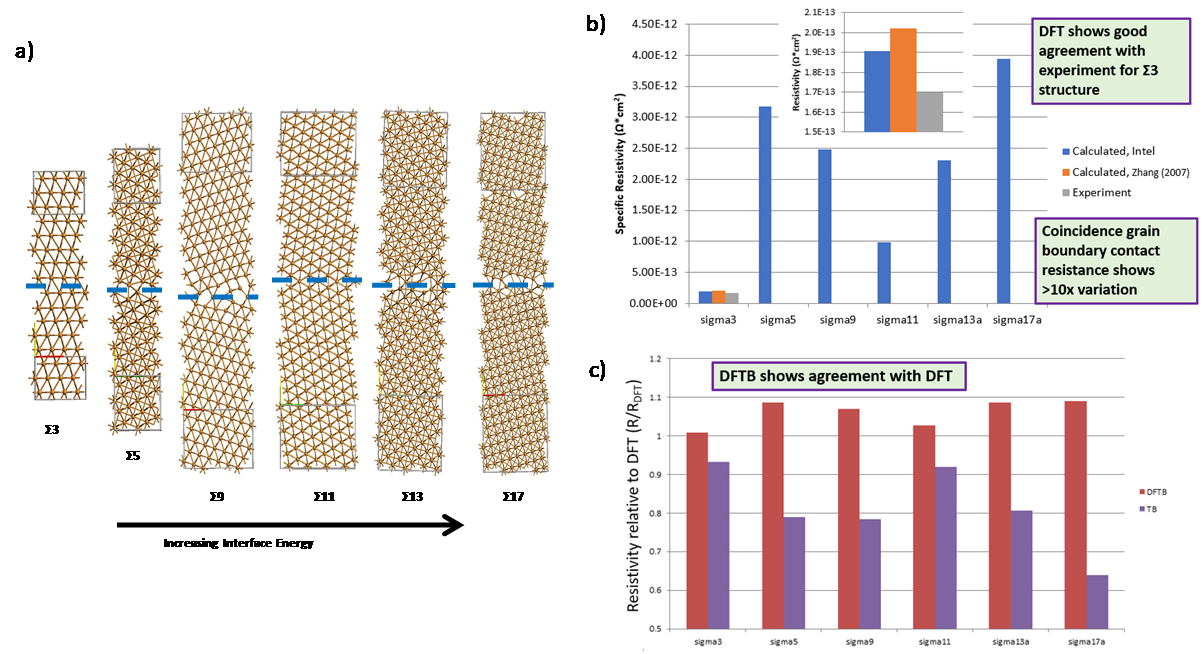
The line resistance of Cu interconnects is shown to be determined by the dimensions, texture and interfaces of the metal. In this section we describe the methodology used to accurately represent the Cu microstructure in planar and trench geometries for use as metal interconnects in integrated circuits. Atomistic representations may be created analytically for bulk and planar polycrystalline configurations, followed by an energy minimization step using LAMMPS
[12]. Figure 4(a) shows the generated polycrystalline representation of different grain orientations and boundary interfaces for the most stable Cu textures, generated by rotating perfect crystals to give a single grain boundary. Resistivity of the structures was calculated from using the Nonequilibrium Greens Functions framework
[45]. Figure 4(b) shows the resistivities calculated using DFT simulations and compared to experimental and external reports
[46]. The computationally faster method of Density Functional Tight Binding (DFTB)
[47] was shown to give similar resistances as DFT simulations (see Figure 4(c)) and can be used for larger multi-grain structures with mixed grain boundary types. It is more accurate than using Tight Binding (TB) with parameters from Papaconstantopoulos
[48].
Figure 4.
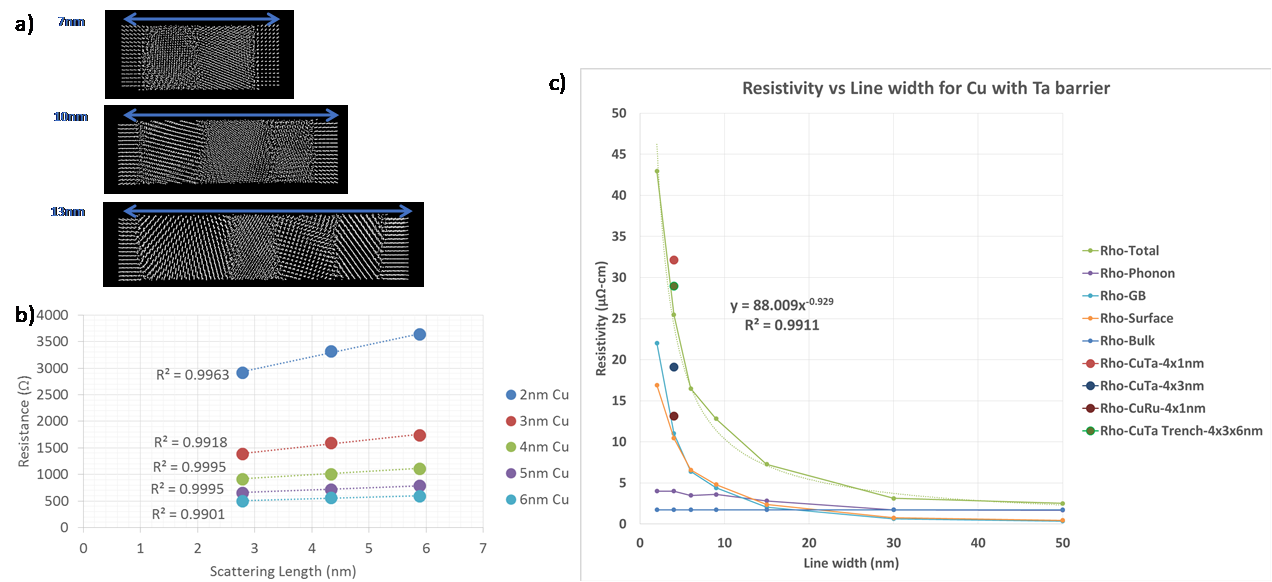
a) Analytically generated polycrystalline FCC Cu grain structures for different sigma grain boundaries. b) calculated resistivity for specific grain boundaries. c) comparison of TB and DFTB resistivity for different grain boundaries relative to DFT. Using larger analytic polycrystalline structure, over 150 configurations with roughly uniform grain sizes averaging from 2-6nm in size for 3 different lengths ranging from 7-13nm long (see Figure 5(a)) were used to calculate transmission. From these length dependent resistance plots shown in Figure 5(b), the resistivity as a function of grain size was extracted, showing smaller grains lead to higher resistivity due to increased scattering at grain boundaries. Assuming grain sizes proportional to line widths, the resistivity of interconnects including the components extracted for GB & surface scattering can be plotted as shown in Figure 5(c) showing the expected rapid increase below 5nm.
Figure 5.
a) examples of analytic polycrystalline Cu structures with perfect leads used as input to DFTB transmission calculations; b) resistance curves for different lengths and average grain sizes; c) extracted resistivity curves for phonon, GB scattering and surface scattering components. Circular points are the values extracted from realistic MD deposition samples on the same plot. While analytic methods can be used to arrange a small amount of grains, MD can be used to simulate the deposition process, enabling the generation of truly realistic microstructures for material property calculations. Figure 6 shows the deposited microstructure results from MD simulations of Cu deposition on Ta substrates using the methodology described by Zhou and Francis
[49, 50] with EAM potentials tuned for binary metal systems. Due to timestep limitations of the MD method, the deposition was simulated at an extremely exaggerated deposition rate (1 adatom/30fsec) at a temperature of 400K in order to get a sufficient thickness of 50 monolayers in the usec timeframe available. Even with the elevated conditions, the resulting (111) FCC grains with 30° rotation were in agreement with experimental reported microstructures
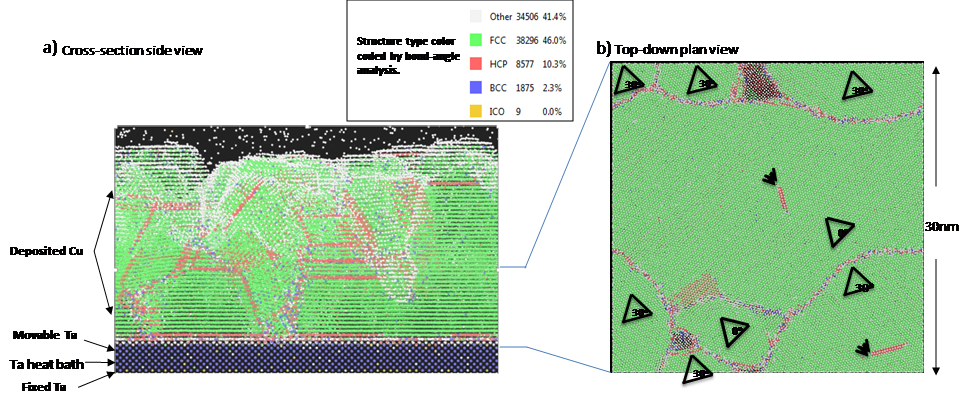
[51].
Figure 6.
Cu atoms deposited on a planar Ta substrate a) side-view showing the Ta substrate layers with deposited Cu atoms; b) top-down view of a slice through the substrate and Cu deposited layer showing the microstructural grains, boundaries, and stacking faults. Multiple instances of these microstructures were then used as input to DFTB transmission calculations to extract the resistivity for grain sizes. Extractions from slices of the realistic planar and trench MD deposition simulations are shown in the datapoints on Figure 5(c), giving good agreement with the analytic extracted curves. It confirms that the analytically generated GB structures are equivalent to the more costly full MD deposited polycrystalline ones, validating the methodology. This shows the power of using a combination of atomistic material modeling tools to generate and analyze microstructural dependence of material properties.