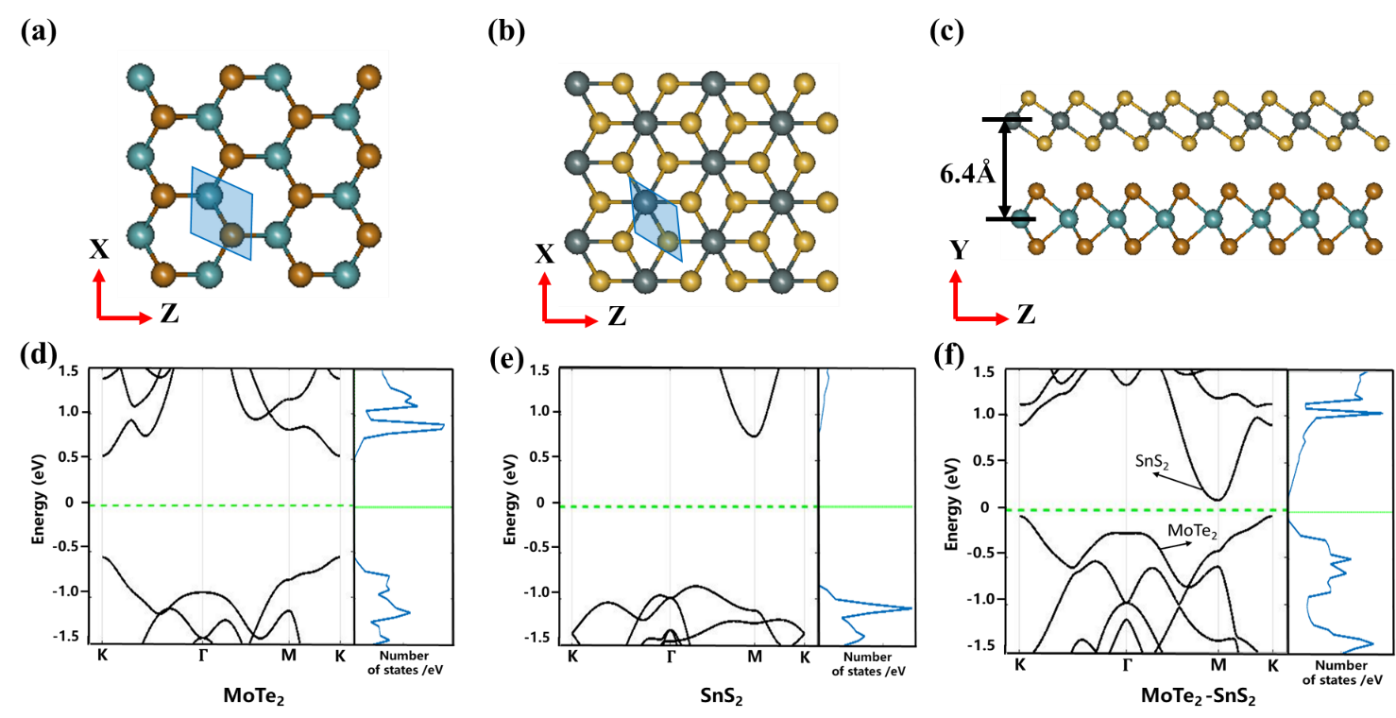
In order to precisely calculate the electronic states properties of the MoTe2-SnS2 heterojunction model, we employ the DFT based ab-initio package Nanodcal. The generalized gradient approximation (GGA) of Perdew, Burke, and Ernzerhof (PBE) is applied for the exchange-correlation interactions, which can exactly present band gap values in good agreement with experiment results for monolayer 2D materials. The energy cutoff is 500 eV and the Monkhorst-Pack k points are set as 9 x 9 x 1 without spin-orbit coupling. The convergence criteria for energy and force are 10-4 eV and 10-3 eV/ Å. The relaxed monolayer MoTe2 and SnS2 are shown in Figure 1 (a) and (b) with the lattice constants being 3.56 Å and 3.70 Å respectively. And the heterostructure is built after applying strain to both two materials so as to obtain the same lattice parameter a0 = 3.625 Å as shown in Figure 1 (c). To study the basic properties of monolayer MoTe2 and SnS2, the band structure of two materials is calculated along the high-symmetry path (K-\(\mathrm{\Gamma }\)-M-K) in Brillouin zones. As shown in Figure 1 (d)-(f), the band structure of intrinsic monolayer MoTe2 has a 1.10 eV direct band gap at K point, like the other traditional 2D semiconductor materials. And monolayer SnS2 has an indirect gap of about 1.61 eV that is an applicable value as the channel material of MOSFETs. Combined two materials, it formed a system that is a type-II heterojunction with a 0.29 eV indirect band gap which is larger than the band gap of another similar combination of 2D material stack, i.e., WTe2-MoS2 (0.16 eV) [23]. Compared all three band structures, it is obvious that the valence band maximum (VBM) is contributed by MoTe2 at K and the conduction band minimum (CBM) is contributed by SnS2 at M. Therefore, if the transport axis is along the M-K direction, the momentum is conserved in the periodic direction and the tunneling process can be formed along the transport direction due to the variation of electrostatic potential.
Figure 1.
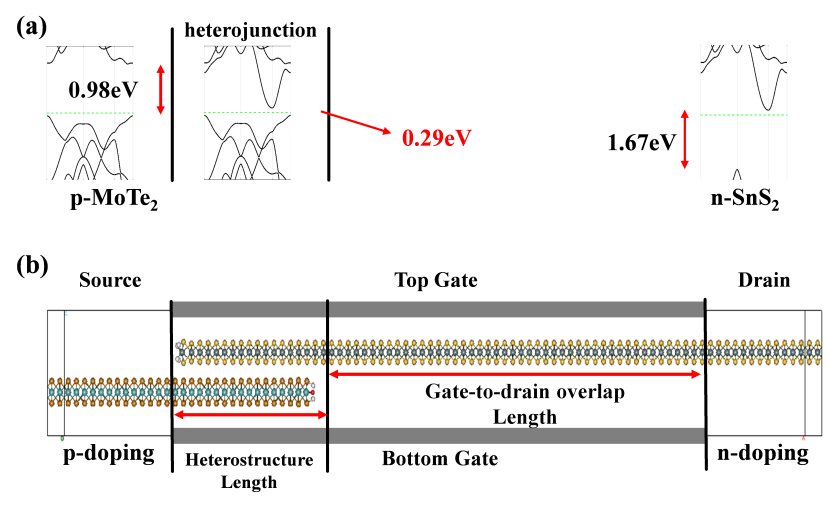
(a-c) basic structure of MoTe2, SnS2 and heterostructure, the permittivity cell is covered by the shadow area contained three atoms; (d-f) Band structure and density of states of intrinsic MoTe2, SnS2 and MoTe2-SnS2 heterostructure. The device band edges schematics demonstrate the mechanism of the MoTe2-SnS2 TFETs as shown in Figure 2 (a). The Type II band alignment can effectively keep the tunneling window of channel. Note that the interaction of the stacking edge has a dramatically deviation of the band structure, as compared with monolayer or heterostructure, which dominate the tunneling on current of the TFET. Longer heterostructure length can hardly enhance the tunneling on current since the bands are rather flat in the middle region, but leads to larger channel resistance. On the other hand, very short heterostructure length also leads to TFEF performance degradation due to the direct source to drain tunneling.
Figure 2.
(a) Band alignment schematic in the device along the transport direction with flat band condition; (b) Schematic of the double-gate MoTe2-SnS2 heterostructure TFETs with gate to drain overlap. To obtain multi-objective optimization for on-state current and off-state current trade-offs, the schematics of TFETs device with gate-to-drain overlap design is presented in Figure 2(b). The distance between MoTe2 and SnS2 layers is 6.4Å,which is optimized by optB86 exchange correlation functional method. To avoid the influence of mismatch, monolayer MoTe2 is applied 2.1% tensile strain and 2.0% compressive strain is for SnS2, which can keep lowest mismatch. For the whole TFET device structure, the total number of atoms exceeds 360. As shown in Figure 2 (b), the out-of-plane vacuum separation of the device is fixed as 2 nm, which is equal to the distance between the top and bottom gates. Spin-orbit coupling is excluded. In our work, we investigate the influence of EOT variation for the performance of TFETs device. The default effective oxide thickness (EOT) is set to 0.5 nm with effective κ=3.9. For the gate voltage, the bias is only applied to the top gate and the bottom is set as ground. In the case of n-type device, the source side is doped to p-type and the drain side is doped to n-type. Both the source and drain doping concentration reach 1013 cm-2. And the intrinsic materials are employed for the channel because the device performance is insensitive to the doping concentrations. The supply voltage is set as Vds = 0.05 V in all the following simulation. In this condition, the self-consistent electrostatic and transport calculation for each gate bias point spends about 18 hours of wall time by using 144 CPU cores.
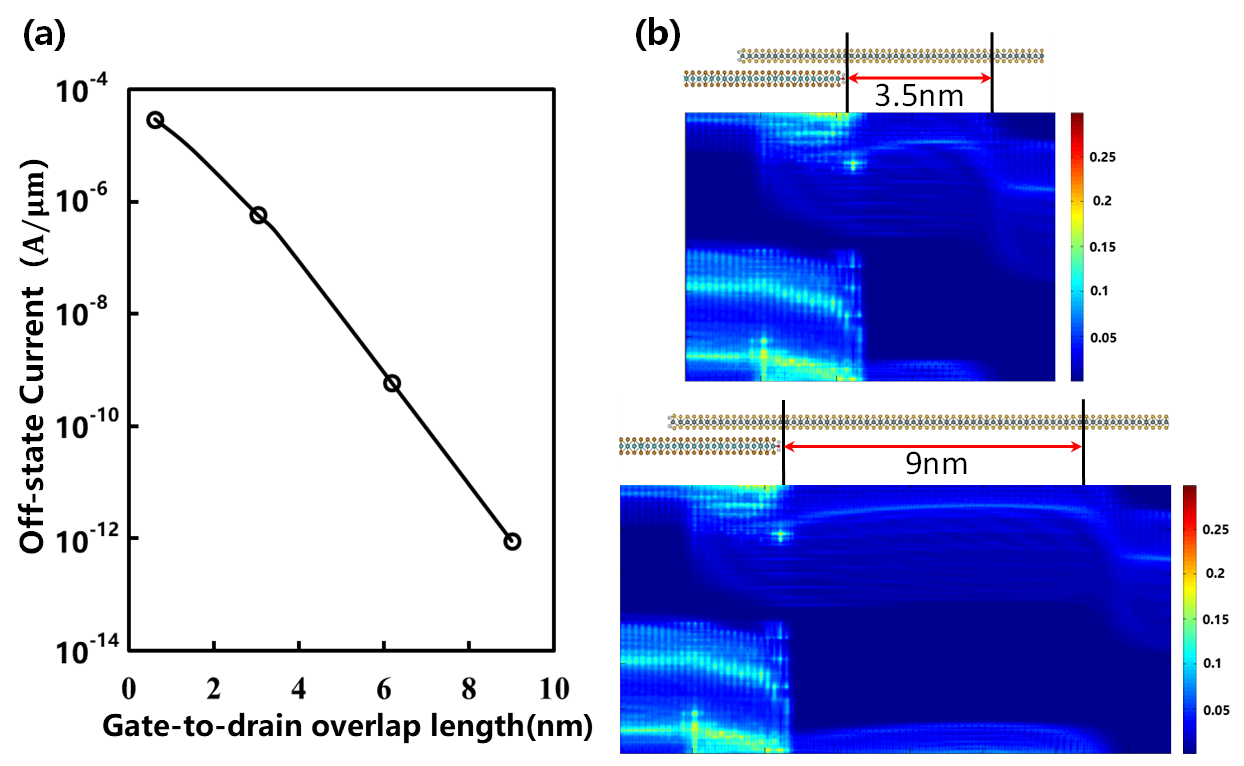
Firstly, we investigate the impact of length variation from heterostructure to drain (gate-to-drain overlap) on the device properties. The heterojunction length is fixed to 3 nm. As shown in Figure 3, the leakage can be effectively reduced with increasing the length of overlap. At Vgs = 0 V, the Off-state current of 4 nm overlap is as large as 10-7A/μm and it can be reduced to 10-13A/μm with 9 nm overlap condition. It indicates that electrons in the VB of MoTe2 have a high probability of tunneling into the CB of SnS2 without gate voltage at short overlap region. The gate-to-drain overlap design gives rise to good optimization for Ion and Ioff trade-offs as compared to normal TFET in previous studies [20] (see Table. 1). The 9 nm gate-to-drain overlap structure is selected as the basic TFET structure to calculate following transport characteristic. In addition, as increasing EOT from 0.5 nm to 1 nm, the performance of TFET device present the degradation tendency, e.g., the subthreshold slope drops to 48 mV/dec and the Ion/Ioff ratio decreases about an order of magnitude. To achieve optimal performance, thin EOT of 0.5 nm is selected in the following calculations.
Figure 3.
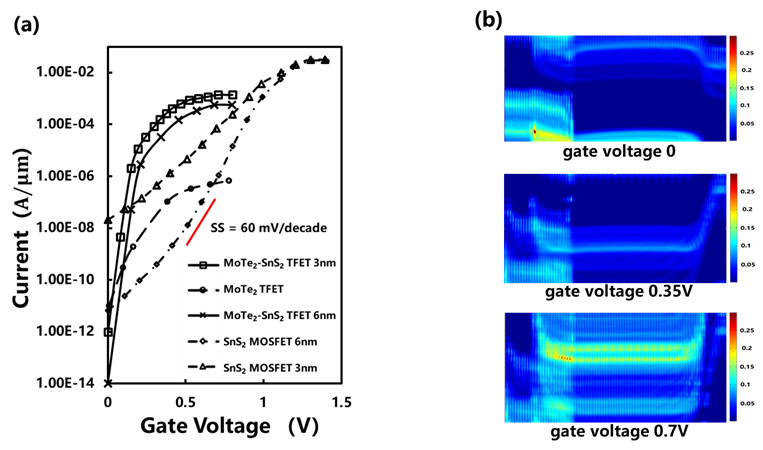
(a) The variation of off-state current with different length of gate-to-drain overlap between heterostructure to drain. With the increasing of length, the leakage of drain can be effectively suppressed at the same supply voltage; (b) LDOS of the TFETs with different gate-to-drain overlap length at Vgs = 0V. Then, the transport properties of n-type device are simulated by the DFT-NEGF method. The Id-Vgs curve of the MoTe2-SnS2 TFETs is shown in Figure 4 (a). It is obviously that the sub 60 mV/decade subthreshold swing is obtained as about 37 mV/decade. By fixing the Off-state current of the device to\({10}^{-6}\mathrm{ }\mathrm{\mu }\mathrm{A}/\mathrm{\mu }\mathrm{m}\), the current can achieve about 20\( \mathrm{\mu }\mathrm{A}/\mathrm{\mu }\mathrm{m}\). For benchmark, the transfer characteristics of a single-layer MoTe2 TFET is also simulated. The SS is not notably below the limitation of MOSFET and the On/Off current ratio only reach to about 105 due to the short channel length. The mechanism of n-type TFETs is demonstrated in Figure 4 (b), which presents the LDOS of the TFETs with the different gate voltage. At Vgs = 0V, tunneling path does not exist because the VBM of MoTe2 is located below the CBM of SnS2 in the channel region, which also proves that the buffer layers of both two side is long enough to keep the minimal impact of the leakage. With the increasing of gate voltages, the CBM of SnS2 is dropped down faster than the VBM of MoTe2, on account of the effectively modulation of SnS2. At Vgs = 0.35V, electrons in the VB of MoTe2 are gradually enter into the CB of SnS2 at the center of the channel. They can tunnel from the source of MoTe2 cell into the drain because the CBM is getting lower in the monolayer than in the heterostructure. In the On-States, the bands of MoTe2 and SnS2 are totally changed in the overlap region when the gate voltage is over 0.4 V. Electrons can freely cross through the whole stacking area at high gate voltage. This indicates that the MoTe2-SnS2 TFETs can have better performance compared with single-layer 2D materials MOSFETs.
Figure 4.
(a) Id -Vgs transfer properties. The solid lines represent the transport characteristics of heterojunction with different heterojunction length region and the dashed lines demonstrate transport properties of single-layer MoTe2 TFET; (b) LDOS of the TFETs with different gate voltages. Based on this result, we further investigate the influence of increasing the heterojunction region length from 3 nm to 6 nm. On one hand, the length of the stacking region cannot markedly enhance the on-state current. On the other hand, it leads to a better control of the off-state current as shown in Figure 5. As the data presented in Table 1, the on-state current of short heterostructure length TFET is similar to the longer heterojunction length. The band-to-band tunneling and the direct source-to-drain tunneling are essential in the tunneling processes. The longer heterojunction length device can be effectively suppressed the leakage arising from the direct source-to-drain tunneling, but does not notably affect the on-state current due to the band-to-band tunneling.
Figure 5.
LDOS of TFETs with different heterojunction length at On/Off states. At Vgs = 0V, the device of 6nm presents more effective. Table 1.
Heterojunction length and corresponding device key merits. | Heterojunction Length (nm) | Ioff (A/μm) | Ion (A/μm) | Ion/Ioff | SS (mV/dec) |
3
(this work) | 2.05E-12 | 5.77E-04 | 108 | 37 |
6
(this work) | 2.38E-14 | 1.46E-04 | 1010 | 42 |
20
[Ref 20] | 1E-12 | 7.5E-5 | 107 | <60 |