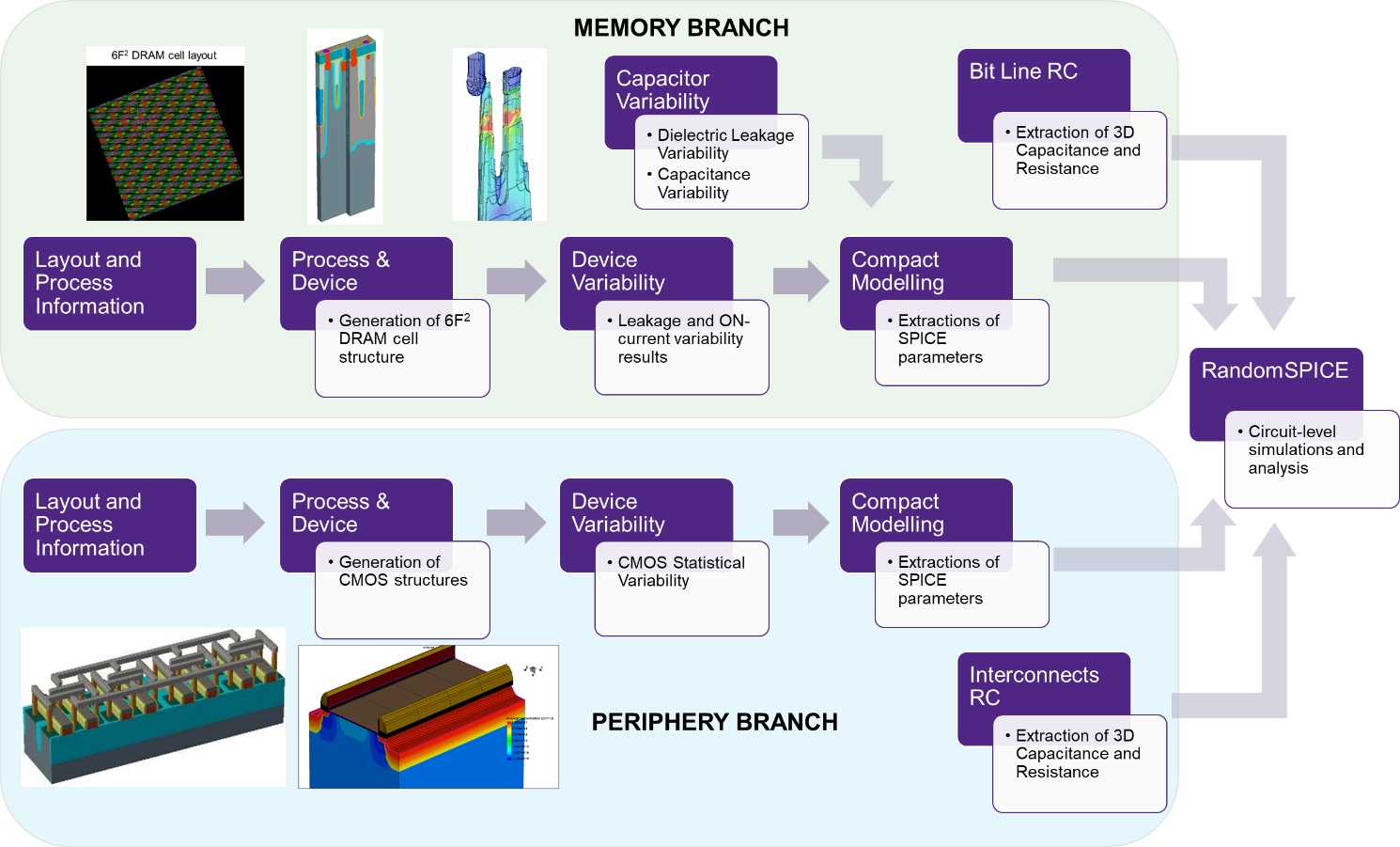
The goal of the simulation-based DTCO flow shown in Figure 1 is to achieve the simulation based estimation and optimization of the DRAM refresh time (tREF) and, in turn, DRAM yield, in presence of process and statistical variability and for a given set of manufacturing assumptions. In this section, we will address the issues limiting tREF at the memory array level, whilst in Section 4 we will focus on the CMOS periphery limitations (Table 1).
3.1. DRAM Transistor – Process and Statistical Variability
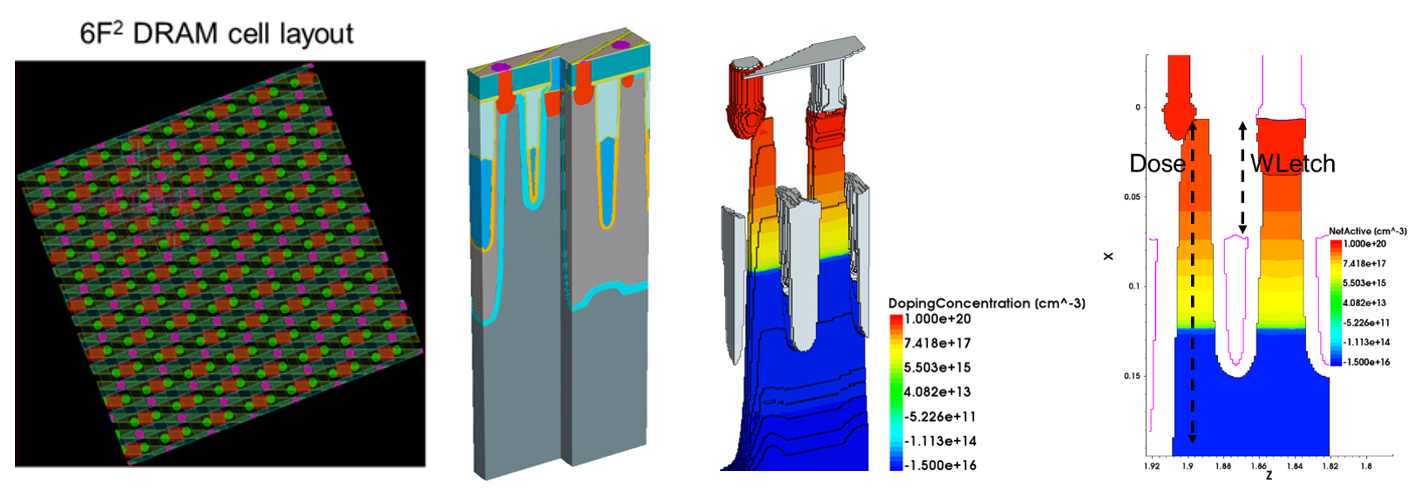
The Synopsys TCAD platform [17–23] is used for the generation and simulation of the 3D DRAM array. The DRAM structures are constructed by means of Process Explorer [17] starting from a 6F2 tilted-cell layout representative of a 2z nm technology node (Figure 2). A single cell and two adjacent neighbors are then cut-out to perform accurate doping implantation and device simulation by means of S-Process [18] and S-Device [19], respectively. Different process conditions are simulated by changing WLetch (WL recess etch) and Dose (roll-off) parameters by +/- 20% (Figure 2) to generate a range of structures corresponding to different process conditions, or process variations. The cell transistor, consisting of a saddle-fin featuring buried metal WL and shared common BL (Table 2), is then re-meshed to enable the statistical simulation of ON and leakage currents by means of the drift-diffusion variability engine Garand VE [20].
It has been previously shown that discrete doping can play a fundamental role in determining the stochastic dispersion of both drive current and leakage current in transistors. In this work, we consider the trap-assisted band-to-band tunneling (TAT) as the dominant contribution to the transistor leakage. The experimental results, in fact, clearly show that the transistor leakage current is a function of the number of defects in silicon, their energy level in the bandgap, and the electric field
[6]. The trap-assisted contribution is modelled through an enhancement of the trap capture cross-section in the conventional Shockley-Read-Hall (SRH) generation term. The enhancement can either be computed by Hurkx-like local models or by non-local tunneling path approaches. For each process corner, Garand VE simulates hundreds of statistical instances. Each instance features a different configuration of random discrete dopants (RDD) and thousands of single-trap positions are evaluated to gather the TAT leakage statistics. Once the single-trap leakage statistics are obtained, any other statistics due to an arbitrary trap density can then be obtained at SPICE level by convolution of the single-trap cumulative distribution functions (as detailed in [
28]).
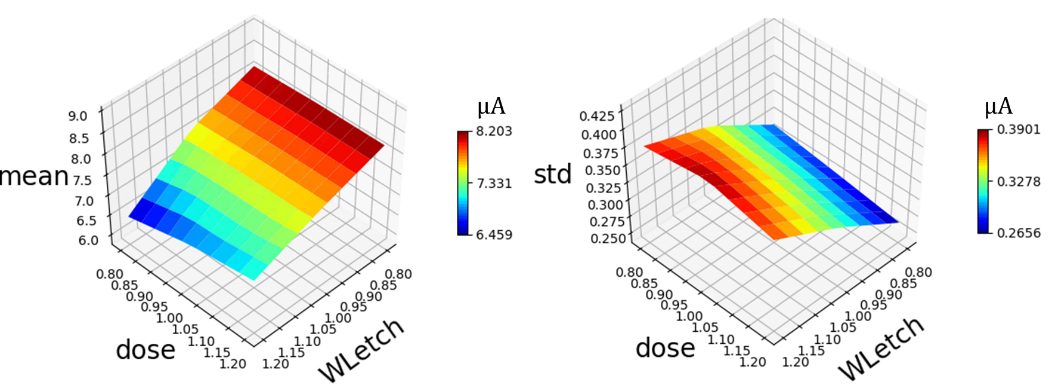
Figure 3.
ON current average (left) and variability (right) performance across the space of process variations. Figure 4.
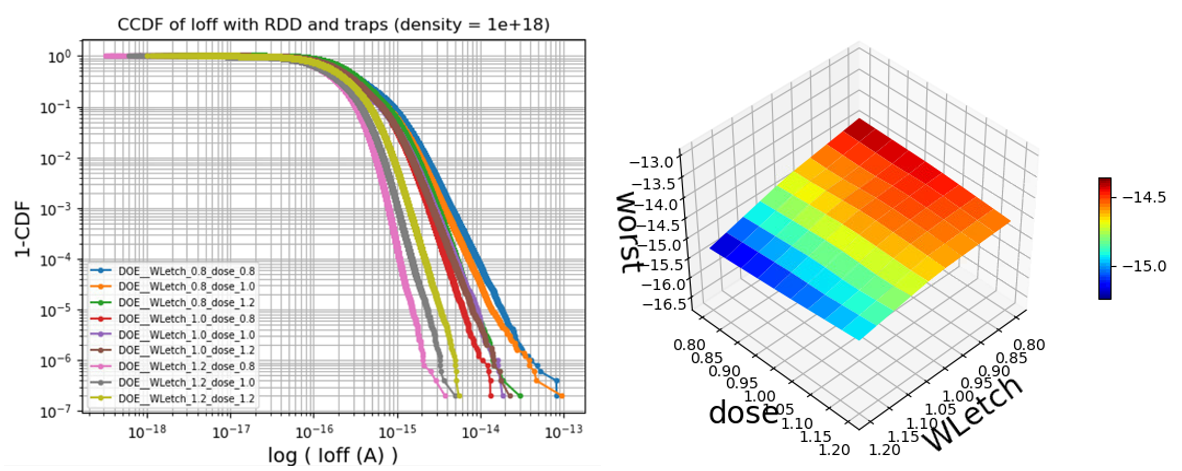
Leakage complementary cumulative distribution for different process corners (left); the worst leakage value is plotted across the space of process variation (right) as measure of the leakage variability. Figure 3 shows the results of the Garand VE analysis performed to evaluate the impact of RDD on the ON-current for the DRAM cell, across the WLetch and Dose process variations space. A 10% variation in the mean ON-current can be observed, whilst the ON-current standard deviation varies from 3% to 6% of the nominal ON-current value. These variations can be understood by considering that the combination of WLetch and Dose define the gate to source/drain overlap. With a high WLetch, there is significant underlap, leading to low ON-current and high variability.
To evaluate the leakage variability, we have performed 200 Garand VE simulations for each process corner. For each RDD configuration, the single-trap TAT leakage is simulated by sweeping the trap position across the drain (storage node contact) pillar region with a 0.5nm spacing, leading to ~70,000 trap evaluations per each RDD configuration (14,000,000 trap configurations for each simulated process condition). Figure 4 shows the leakage complementary cumulative distribution, highlighting that the interaction between discrete traps and random dopants leads to extended exponential-like tails. Moreover, both average and tail behavior strongly depend on the process variations. It is important to note that the variability of ON-current is anti-correlated to the variability of leakage. Therefore, the best process corner that minimizes ON-current variability is also be the worst corner that maximizes leakage variability. This imposes a trade-off between ON-current and leakage performance and, in turn, between DRAM write time (tWR) and tREF performance.
Once the statistical TCAD results are obtained across the space of process variations, compact models can be extracted by means of a response surface methodology in Mystic [21], as detailed and validated in [28]. It is worth remarking that the leakage due to many random traps can be obtained analytically by self-convolution of the single-trap statistics.
3.2. DRAM Capacitor Dielectric Leakage – Statistical Variability
DRAM capacitors utilize high-k dielectrics to maximize capacitance for a given technology node. Defects in high-k materials may cause undesirable leakage currents due to trap assisted tunneling. The leakage currents in the capacitors in a memory device have been one of the bottlenecks for further scaling down. Therefore, a systematic way of modeling and understanding the trap assisted tunneling transport mechanisms is required to support further downscaling.
To calculate the leakage current for a metal-insulator-metal structure, we have developed a stochastic reliability simulator, Sentaurus Device KMC
[19], based on the kinetic Monte-Carlo method. The simulator randomly distributes discrete defects in insulator regions of a 3D capacitor structure. These discrete defects act as traps of carriers in an insulator that can affect device reliability. To simulate the electron transport via the traps, the electron hopping event rates are calculated with various physical models
[29], including direct tunneling, Fowler-Nordheim (FN) tunneling, inelastic multi-phonon trap-to-trap and trap-to-electrode tunneling
[30], and Poole-Frenkel (PF) emission
[31]. The direct tunneling and FN tunneling are leakage currents without traps; they are determined by the intrinsic insulator properties. With the traps in an insulator, the inelastic multi-phonon processes dominate the tunneling current. These processes involve the emission and absorption of multiple phonons. In the PF emission, the localized electron in a trap is thermally excited to the conduction band of an insulator. Furthermore, the potential energy distribution is calculated by solving the Poisson equation with the image charge barrier lowering near electrodes as well as the short-ranged trap potentials.
With the KMC method, all possible electron transport events are considered as stochastic process
[32]. The steady state current I_k is calculated by counting the net electrons at the electrode ΔN_k within Δt by I_k=(qΔN_k)/Δt, when the stochastic process reaches steady states.
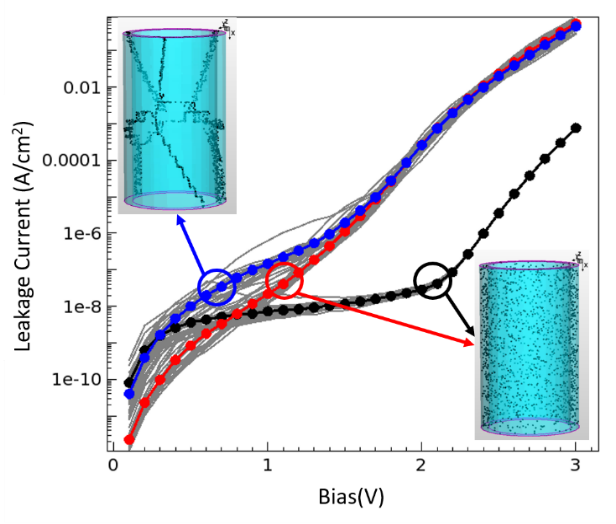
Figure 5 shows the trap assisted tunneling current as a function of the electric field in a HfO2 capacitor. The thickness of the HfO2 layer is 5nm, and the outer diameter of the cylinder is 60nm. The electrodes are TiN. The leakage currents are compared according to the solid states of the insulator, i.e., monocrystalline, amorphous, and polycrystalline HfO2. For the monocrystalline and amorphous HfO2, the traps are randomly distributed in the bulks where the trap concentrations are 2×1019 cm-3 and the trap locations are identical for both structures. For the polycrystalline HfO2, the same number of traps are distributed only on the grain boundaries, which result in smaller trap-to-trap distances in the polycrystalline HfO2. For the crystalline HfO2, a constant trap level, 1.8 eV is used for all traps. In amorphous and polycrystalline HfO2, the trap levels are randomly defined with the Gaussian distribution of the average 1.8 eV and the standard deviation 0.5 eV. In the comparison of the leakage currents in the monocrystalline and amorphous HfO2, the leakage current in the monocrystalline HfO2 is larger than the one in the amorphous HfO2 for low bias, while the leakage current in the amorphous HfO2 becomes larger as the bias increases. For low bias, the inelastic tunneling requires more phonons in the amorphous HfO2 as compared with the monocrystalline HfO2, because the energy differences between the traps are zero in the monocrystalline HfO2. For high bias, the number of phonons for the inelastic tunneling process increases linearly as the electric field increases in the crystalline HfO2, while the tunneling paths requiring fewer phonons can be found in amorphous HfO2 where the trap levels vary over space.
In comparison of the leakage currents in the monocrystalline and amorphous HfO2, the leakage current in polycrystalline HfO2 is larger for the bias below 1.5 V, while the averaged leakage currents are almost identical for both cases when the bias gets higher. For high bias, the single-trap assisted tunneling processes, i.e. electrode-to-trap and trap-to-electrode tunneling, dominate the leakage current. Thus, both leakage currents of amorphous and polycrystalline HfO2 are similar. However, for low bias, in the polycrystalline HfO2, the leakage current is dominated by trap assisted tunneling which is the trap-to-trap tunneling process because of smaller trap-to-trap distances on the grain boundaries. It results in larger leakage current in the polycrystalline HfO2 than one in the amorphous HfO2.
For this simplified example, the capacitor leakage is significantly lower than the transistor leakage, although this may not hold true for more realistic structures and with advanced scaling. Therefore, this KMC analysis represents an important step for the accurate optimization of the DRAM tREF by means of a TCAD-based DTCO platform.
Figure 5.
Leakage current in cylinder capacitors. Black line: Averaged current in the crystalline insulator, traps are randomly distributed in the bulk with the same trap energy of 1.8eV. Red line: Averaged current in the amorphous insulator, traps are randomly distributed in the bulk. Blue line: Averaged current in the polycrystalline insulator, traps are randomly distributed only on grain boundaries. Figure 6.
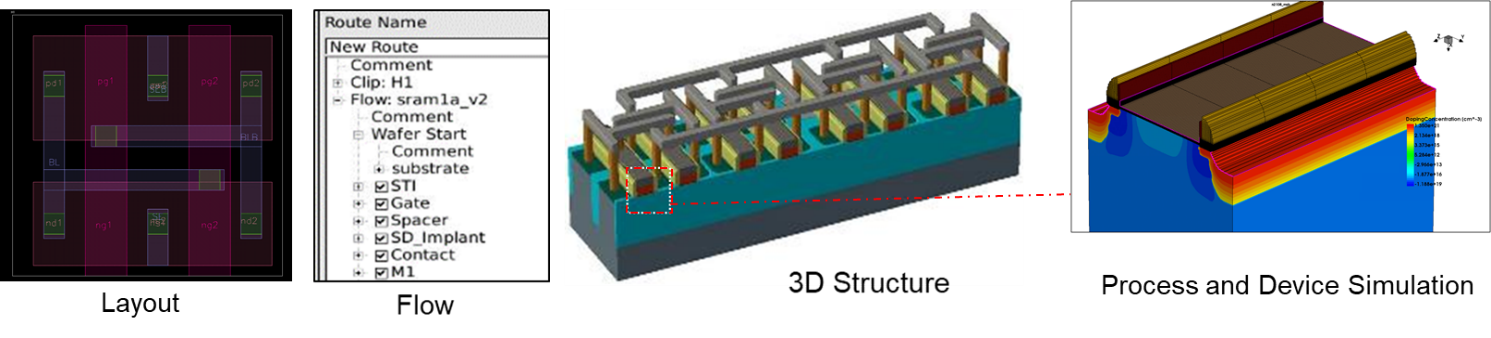
Cell Array RC Extraction. The extraction flow starts from a layout-based structure generation by means Process Explorer. Clips are user-specified to identify the domains of RC extraction, which is then performed by Raphael FX. 3.3.
Cell Array RC Extraction
In the previous sections we have shown how to evaluate the transistor ON-current and leakage and their stochastic dispersions. These TCAD data can be brought to SPICE level via a compact model and a circuit simulation can be performed to obtain outputs such as the DRAM writing time or refresh time. However, this task cannot be achieved without an accurate extraction of the RC parasitics, including bitline (BL) capacitance and the world line (WL) resistance. The cell array capacitance and resistance extraction are performed by using Raphael FX [22], a 3D field solver, therefore offering the highest accuracy for the RC extraction. Moreover, thanks to distributed processing (DP), the tool can keep run-time at optimal levels enabling, for example, the RC extraction of large areas within hours (instead of days). The resistance extraction accuracy is also increased by including surface scattering effect that will lead to an increased resistivity when metal lines cross-sections are scaled down.
Figure 6 shows the cell Array RC extraction flow starting from a layout-based structure generation by means of Process Explorer. Clips are user-specified to identify the domains of the RC extraction, which is then performed by Raphael FX. Table 3 reports single cell capacitance and resistance extracted values. It is worth noting that the BL to SN capacitance dominates the total (~100aF), whilst the BL to BL coupling is relatively weak (~1aF) and the BL to WL coupling is negligible (0.01aF). The WL resistance is around 17 Ohms across the area of extraction. These results will be included in the statistical SPICE analysis presented at the end of Section 4.