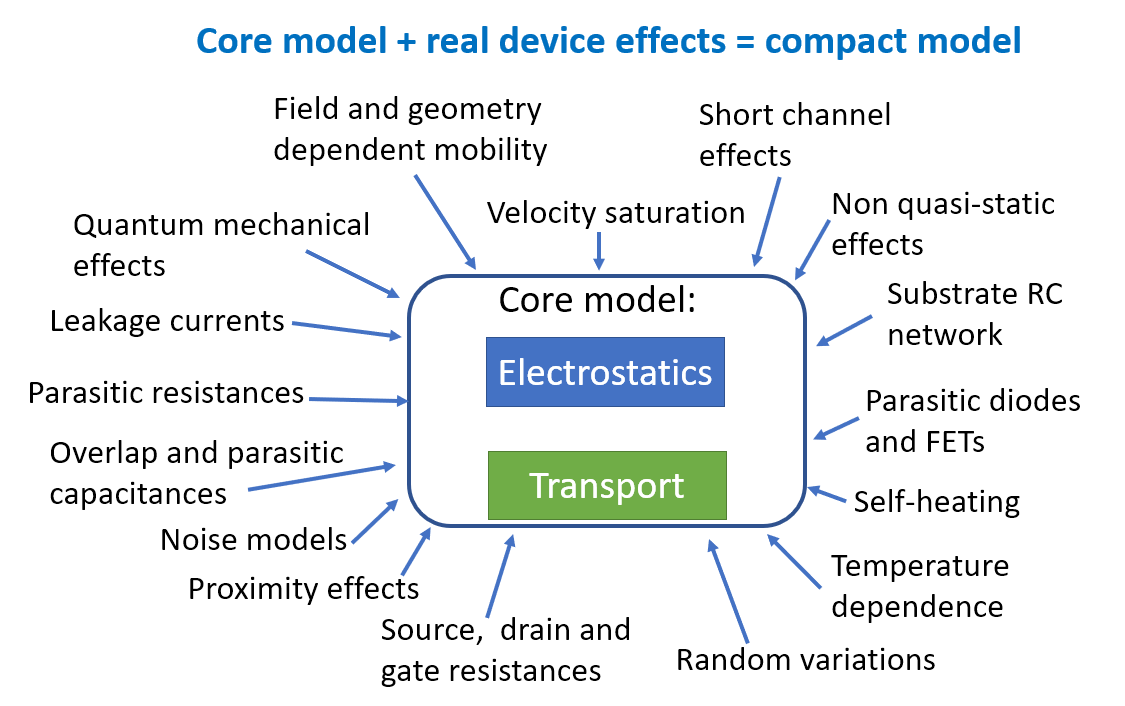
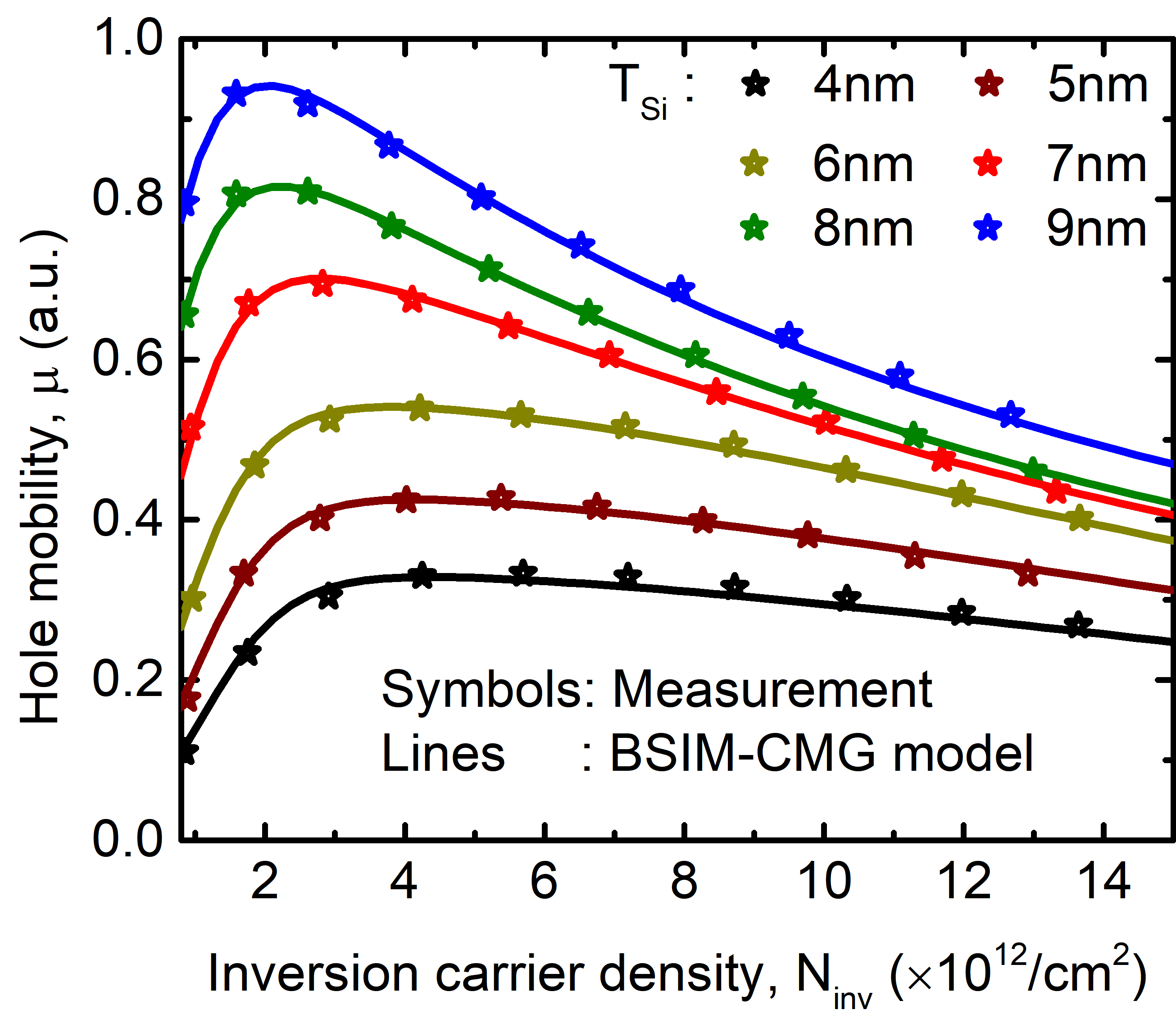
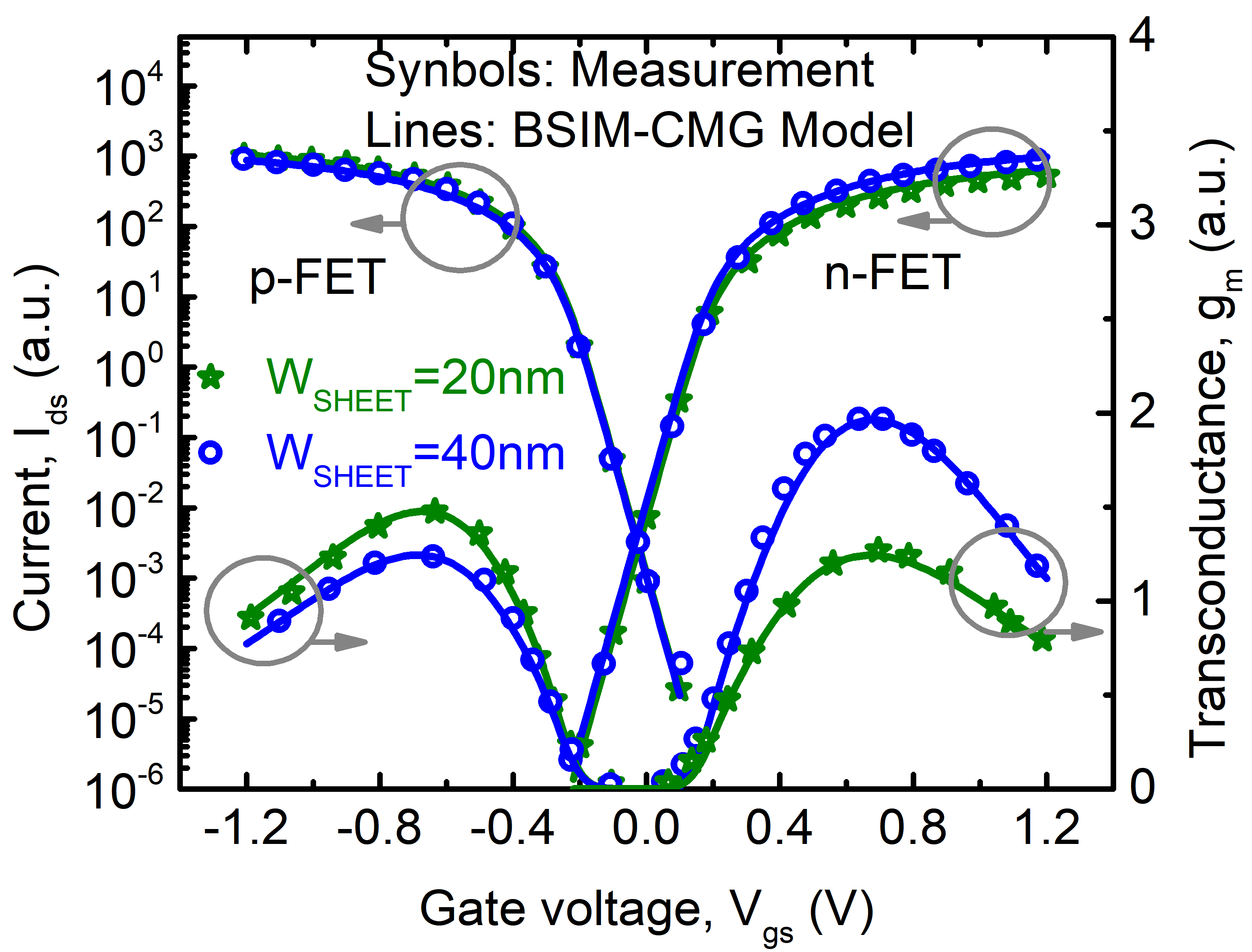
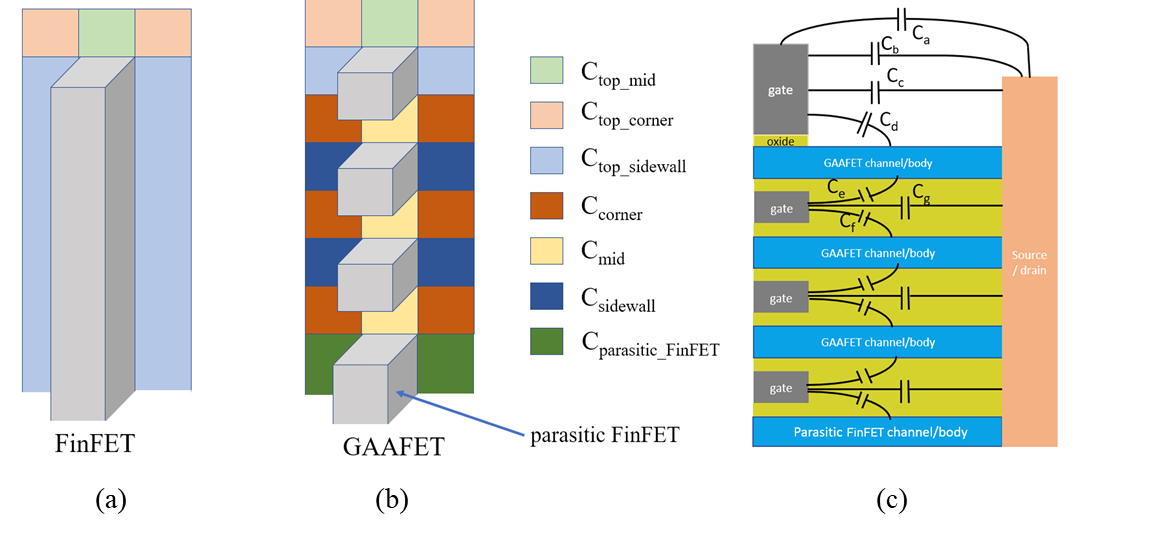
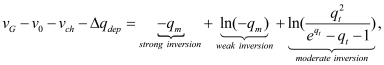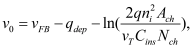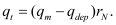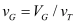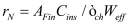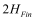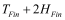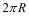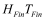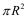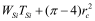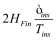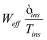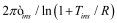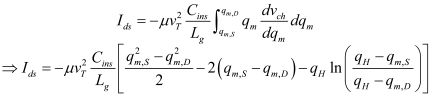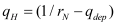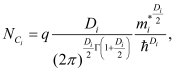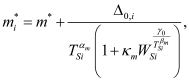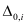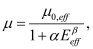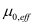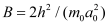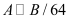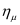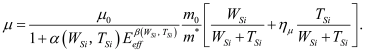BSIM-CMG, through a geometry module (GEOMOD=5), can calculate accurate values of Ach , Cins and Weff ; which are then used in the core model to get the electrostatic behavior, as described in Section 2. The calculation of Ach and Weff include the effects of rounded corners (Figure 1). This model also has the ability to accurately simulate multiple GAA bodies in a single fin (stack). The user can specify various geometry details like the width and thickness of the GAA bodies, the separation between GAA bodies, the number of GAA bodies per fin, fin height etc. The model takes all this geometry information to calculate the electrostatics accordingly. The model can also account for geometry variation among the GAA bodies inside a single fin. In addition to accounting the aforementioned geometry variations, the model further supports Monte Carlo circuit simulation to account for the stochastic device geometric variations that may be encountered in manufacturing.
A significant impact of the confined channel of GAAFETs is the quantum confinement effect on the density of states of silicon. This affects the bias dependence of the channel mobile charge; which in turn affects all device characteristics. To understand the various quantum mechanical effects that play a role, consider the charge in a semiconductor, which can be written as

(6)
where
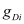
is the density of states for the
ith subband,
Ef is the fermi energy and
Fj () is the Fermi integral of order
j. The term,
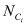
, is given as
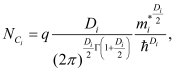
(7)
where
Di is the electrostatic dimension for the
ith subband,

is the effective mass of the
ith subband and

is the Planck’s constant. In BSIM-CMG, the user is allowed to choose up to 3 subbands and can modify individual subband parameters (refer Table 2).
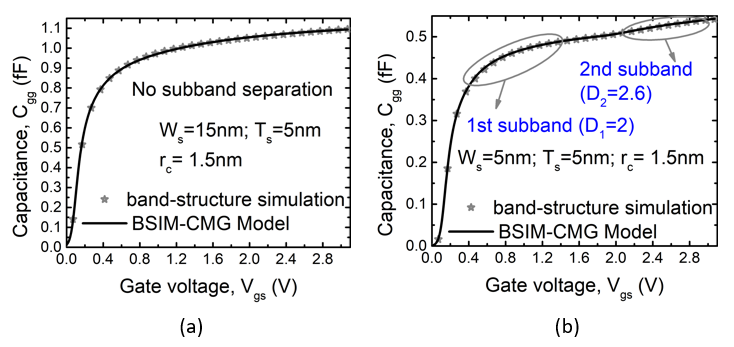
Figure 3.
The plots show the gate capacitance with varying gate voltage; for channel thickness of 5nm. For larger cross-sections, like in (a), the confinement is non-existent. Extreme width confinement, as shown in (b), results in a small effect of subband separation. Figure 4.
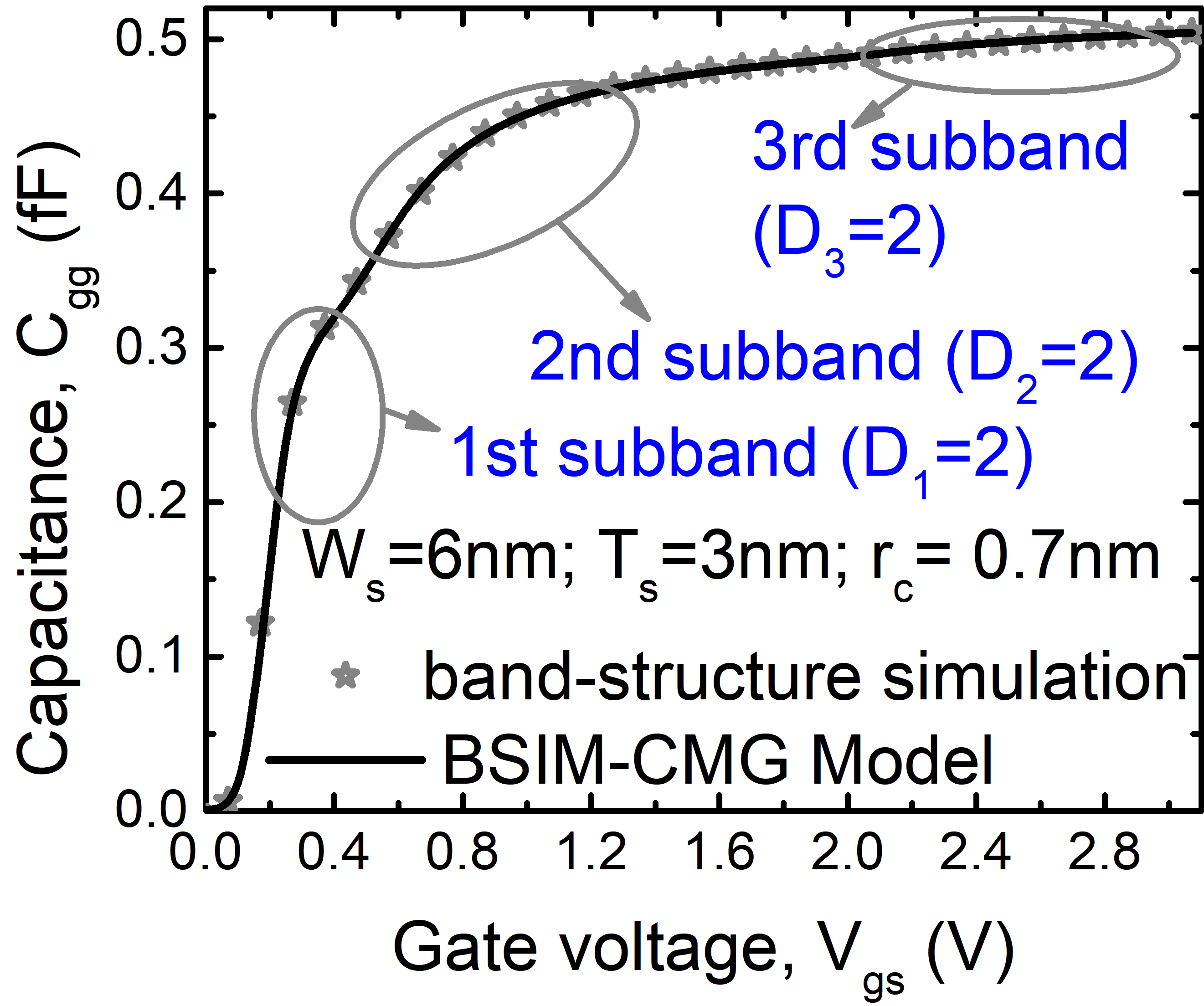
The plot shows the gate capacitance with varying gate voltage; for channel thickness of 3nm. For confined widths, the subband effects are quite pronounced and the overall electrostatic dimension reduces to 2D. With changing cross-section, the electrostatic dimension Di changes. It was recently pointed out that while 1D and 2D are popular and important special cases of quantum confined state, the electrostatic dimension can be a continuous variable. BSIM-CMG is the first compact model that accounts for this fact and can therefore accurately model GAAFET for continuously variable width, WSi [13] . For very confined channels, the system generally has lower dimension. For example, thin and wide channels behave as 2D systems whereas thin and narrow channels are confined in the width direction also, resulting in a 1D behavior. With decreasing confinement, the dimension gradually changes to higher values (2D/3D). This behavior is shown in Figure 3, Figure 4, and Figure 5, where the plots show capacitances (which mimic the density of states) for various cross-sections. As confinement reduces, the dimension shifts from lower to higher values.
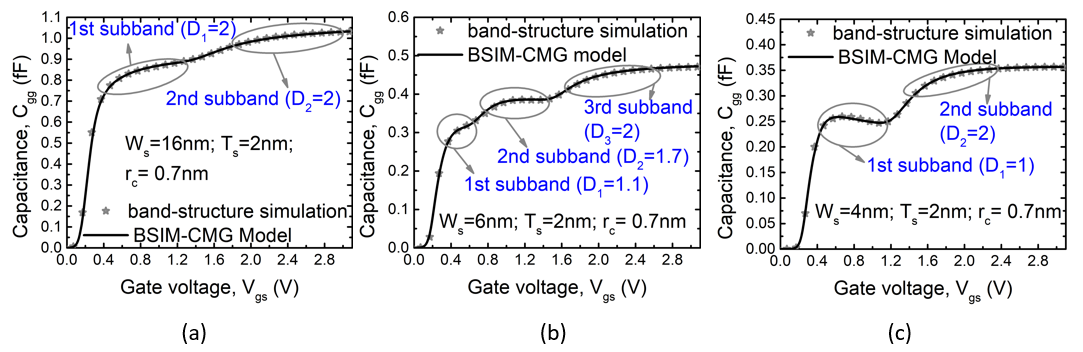
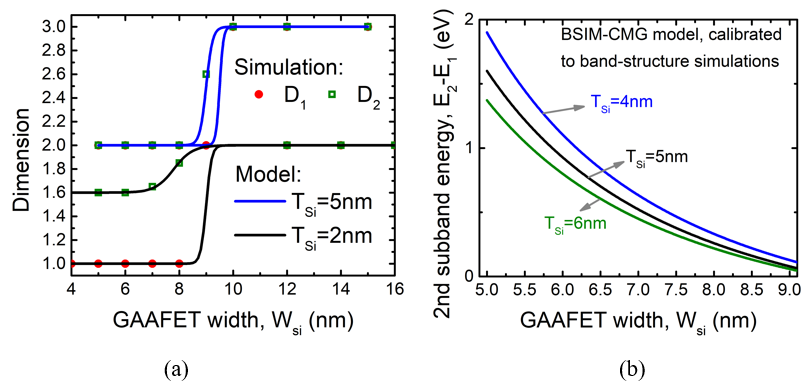
Figure 4 and Figure 5 also shows peaks and valleys in the capacitance. These occur due to subband separation. For very confined devices, the conduction band splits up into subbands resulting in peaks in the density of states; which are reflected in the capacitance plots. With increasing confinement, the subband energies increase and they move further apart as illustrated in Figure 5. For larger cross-sections the subband energies reduce and they come closer in energy; forming continuous conduction band. The subband model has been discussed in detail in [13].
Figure 5.
The plots show the gate capacitance with varying gate voltage; for different GAAFET thickness=2nm. The confinement changes from 2D to 1D with decreasing GAAFET width. Figure 6 (a) shows the variation of the electrostatic dimension with changing GAAFET width for 2nm thick channels (black line). As confinement reduces with increasing width, the dimension changes from 1D to 2D. The maximum dimension is restricted by the thickness confinement (2nm) and is hence limited to 2D. For thicker GAAFET devices (5nm) the maximum dimension goes up to 3D, as shown by the blue lines. Figure 6 (b) shows the variation of the second subband energy for different cross-sections.
The capacitance (or charge) also depends on the effective mass, as shown in Equation (6) and Equation (7). The effective mass changes with confinement, and so does the bandgap. The effective mass contributes not only to the charge but also affects mobility. However, the effective mass formulations used in the electrostatics and transport are different. For both these effective mass calculations, we have parameters to modify the geometry dependence based on the device type, material, etc. The geometry dependence of the effective mass for the i-th subband in electrostatics calculations is given as
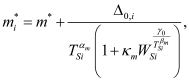
(8)
where
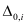
, γ
0,
αm ,
βm and
κm are device dependent parameters.
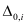
can be used as a fitting parameter to tune the variation of effective mass for each subband. Note that the variation of effective mass in Silicon is quite complex since longitudinal and transverse masses react differently to confinement. However, for compact modeling purposes, we use have developed a single expression for geometry dependence of effective mass for electrostatics which has been described in Equation (8)
[13].
The bandgap on the other hand plays a role in deciding the threshold voltage. With increasing confinement, both the bandgap and the effective mass increase. This increases the threshold voltage and reduces the amount of charge at a given voltage; as can be seen in Figure 5, Figure 4, and Figure 3.
Figure 6.
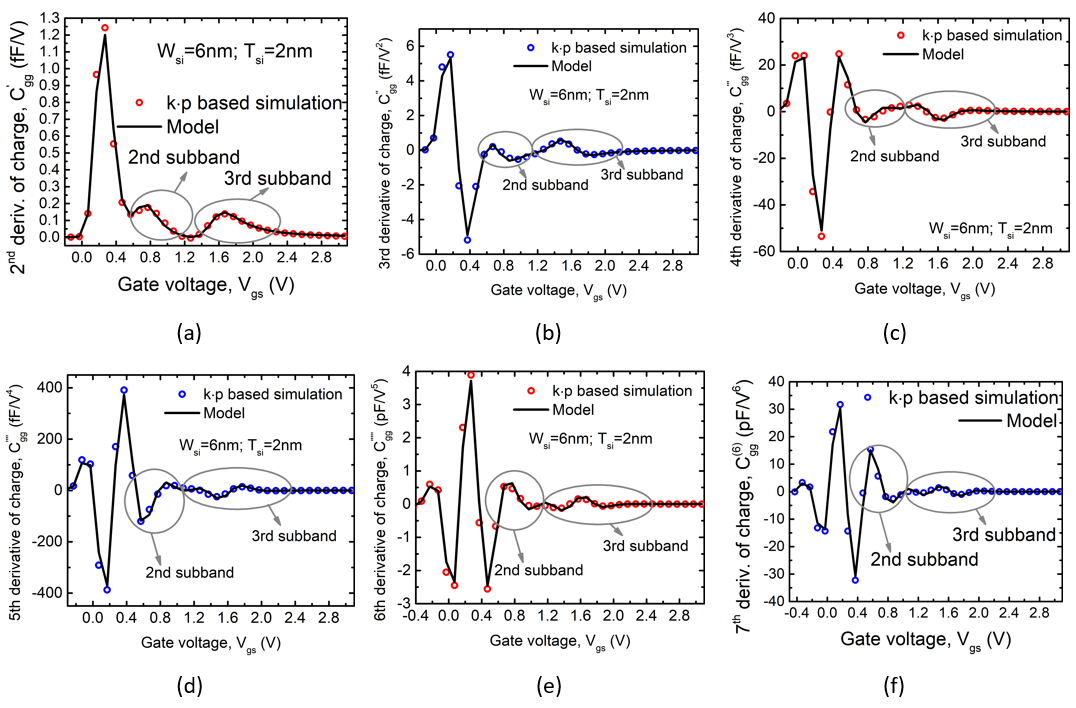
(a) Variation of dimensions for the first and second subbands with thicknesses of 2nm (black lines) and 5nm (blue lines). (b) Variation of the second subband energy, with respect to the first subband energy, for various GAAFET widths and thicknesses. Another key requirement from the compact model is accuracy for derivatives of charges and currents. The peaks and valleys due to quantum confinement lead to multiple secondary peaks in the derivatives of charges. It is important that the compact model captures this to ensure high accuracy for analog/RF simulations. We have developed and tested our model up to the seventh derivative of charge to ensure high accuracy in non-linearity and harmonics simulations. Figure 7 shows the model results for multiple orders of derivatives along with the simulation results to validate this.
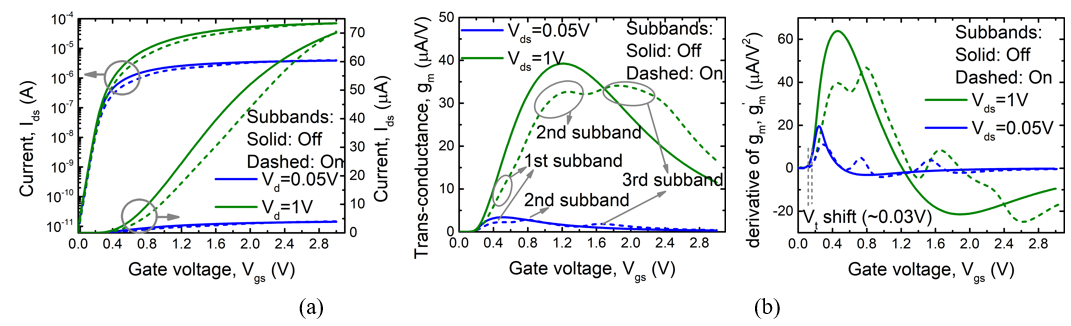
The impact of confinement can also be seen in terminal currents. Figure 8 shows the drain-to-source current along with the transconductance and the derivative of the transconductance for WSi =6nm and TSi =2nm. The simulation has been done with a constant mobility to remove the effects of confinement on mobility. Impact of electrostatic confinement can be clearly seen in plots. Not only does the current reduce due to lower density of states, the effect of subband separation is also seen as distinct peaks and valleys in the derivatives.
Figure 7: Derivates of charge from 1st to 7th order showing the accuracy of the model for higher order derivatives.
Figure 8.
Variation of (a) drain current, (b) transconductance and (c) derivative of transconductance with gate voltage. The solid and dashed lines are the simulation results with and without quantum confinement effects.